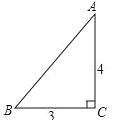
【题目】如图，一张三角形纸片ABC，其中∠C=90°，AC=4，BC=3．现小林将纸片做三次折叠：第一次使点A落在C处；将纸片展平做第二次折叠，使点B落在C处；再将纸片展平做第三次折叠，使点A落在B处．这三次折叠的折痕长依次记为a，b，c，则a，b，c的大小关系是（ ）

A．c＞a＞b B．b＞a＞c C．c＞b＞a D．b＞c＞a

参考答案：

【答案】D

【解析】

试题分析：（1）图1，根据折叠得：DE是线段AC的垂直平分线，由中位线定理的推论可知：DE是△ABC的中位线，得出DE的长，即a的长；（2）图2，同理可得：MN是△ABC的中位线，得出MN的长，即b的长；（3）图3，根据折叠得：GH是线段AB的垂直平分线，得出AG的长，再利用两角对应相等证△ACB∽△AGH，利用比例式可求GH的长，即c的长．

第一次折叠如图1，折痕为DE， 由折叠得：AE=EC=AC=×4=2，DE⊥AC ∵∠ACB=90° ∴DE∥BC

∴a=DE=BC=×3=

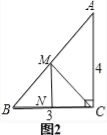
第二次折叠如图2，折痕为MN， 由折叠得：BN=NC=BC=×3=，MN⊥BC ∵∠ACB=90° ∴MN∥AC

∴b=MN=AC=×4=2

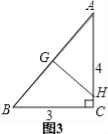
第三次折叠如图3，折痕为GH，由勾股定理得：AB==5

由折叠得：AG=BG=AB=×5=，GH⊥AB ∴∠AGH=90°∵∠A=∠A，∠AGH=∠ACB

∴△ACB∽△AGH ∴= ∴= ∴GH=，即c= ∵2＞＞ ∴b＞c＞a

关闭