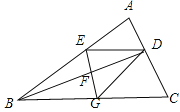
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
参考答案:
【答案】(1)四边形EBGD是菱形;(2)10.
【解析】
试题分析:(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,∴EB=ED,GB=GD,∴∠EBD=∠EDB,∵∠EBD=∠DBC,∴∠EDF=∠GBF,在△EFD和△GFB中,∵∠EDF=∠GBF,∠EFD=∠GFB,DF=BF,∴△EFD≌△GFB,∴ED=BG,∴BE=ED=DG=GB,∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=![]() ,∴EM=
,∴EM=![]() BE=
BE=![]() ,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=
,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=![]() ,MN=DE=
,MN=DE=![]() ,在RT△DNC中,∵∠DNC=90°,∠DCN=45°,∴∠NDC=∠NCD=45°,∴DN=NC=
,在RT△DNC中,∵∠DNC=90°,∠DCN=45°,∴∠NDC=∠NCD=45°,∴DN=NC=![]() ,∴MC=
,∴MC=![]() ,在RT△EMC中,∵∠EMC=90°,EM=
,在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=
.MC=![]() ,∴EC=
,∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,∴HG+HC的最小值为10.
-
科目: 来源: 题型:
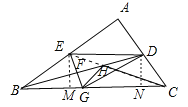
查看答案和解析>>【题目】由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:
①两条对角线互相平分且相等的四边形是菱形;
②菱形的一条对角线平分一组对角;
③若三条线段平方之比是1:1:2,则它们组成一个等腰直角三角形;
④两条对角线互相平分的四边形是矩形;
⑤平行四边形对角线相等.
真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示,则符合这一结果的实验可能是( )
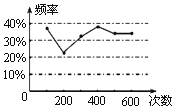
A.掷一枚正六面体的骰子,出现5点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( )
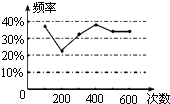
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的一元二次方程x2+(2m﹣1)x﹣3m=0的一个根,求m的值及方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据3,1,5,3,4的众数为( )
A.3B.2.5C.4D.5
相关试题

