【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0②当-1≤x≤3时,y<0③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2④9a+3b+c=0其中正确的是( )
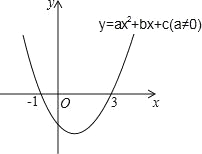
A.①②④ B.①④ C.①②③ D.③④
参考答案:
【答案】B.
【解析】
试题解析:①∵函数图象的对称轴为:x=-![]() =1,
=1,
∴b=-2a,即2a+b=0,故①正确;
②∵抛物线开口方向朝上,
∴a>0,
又∵二次函数y=ax2+bx+c的图象与x轴交点为(-1,0)、(3,0),
∴当-1≤x≤3时,y≤0,故②错误;
③∵抛物线的对称轴为x=1,开口方向向上,
∴若(x1,y1)、(x2,y2)在函数图象上,当1<x1<x2时,y1<y2;当x1<x2<1时,y1>y2;
故③错误;
④∵二次函数y=ax2+bx+c的图象过点(3,0),
∴x=3时,y=0,即9a+3b+c=0,故④正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1是方程ax2+bx+c=0的解,则( )
A. a+b+c=1 B. a-b+c=0
C. a+b+c=0 D. a-b-c=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
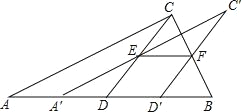
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x2=-2的说法,正确的是( )
A. 由于x2≥0,故x2不可能等于-2,因此这不是一个方程
B. x2=-2是一个方程,但它没有一次项,因此不是一元二次方程
C. x2=-2是一个一元二次方程
D. x2=-2是一个一元二次方程,但不能解
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、En,分别记△BCE1、△BCE2、△BCE3…△BCEn的面积为S1、S2、S3、…Sn.则Sn= S△ABC(用含n的代数式表示).
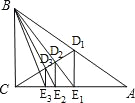
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(4,3)和B是坐标平面内的两个点,且它们关于直线x=-3轴对称,则平面内点B的坐标是( )
A.(1,3)
B.(4,1)
C.(4,3)
D.(-10,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 周长相等的两个三角形一定全等B. 面积相等的两个三角形一定全等
C. 能够完全重合的两个三角形全等D. 所有的等边三角形全等
相关试题

