【题目】如图1,抛物线![]() 与x轴交于A(1,0),B(4,0),与y轴交于点C.
与x轴交于A(1,0),B(4,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)抛物线上一点D,满足![]() ,求点D的坐标;
,求点D的坐标;
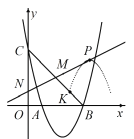
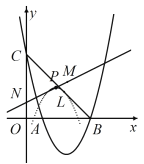
(3)如图2,已知N(0,1),将抛物线在点A、B之间部分(含点A、B)沿![]() 轴向上翻折,得到图象T(虚线部分),点M为图象T的顶点,现将图象T保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围.
轴向上翻折,得到图象T(虚线部分),点M为图象T的顶点,现将图象T保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围.


参考答案:
【答案】(1)y=x2-5x+4;(2) D(![]() ;(3)
;(3) ![]()
【解析】试题分析:(1)待定系数法解抛物线的解析式;
(2)分两种情况讨论:当D在直线AC的左侧时和当D在直线AC的右侧时,求得点D的坐标;
(3)两种极值情况求得m的值,两值之间范围即符合题意
试题解析:
(1)将A(1,0),B(4,0)代入抛物线![]() 的解析式得:
的解析式得:
![]()
解得:b=-5,c=4
∴抛物线的解析式为:![]()
(2)∵A(1,0),C(0,4)
∴直线AC的解析式为![]()
当D在直线AC的左侧时,∵![]()
∴OD∥AC
∴直线OD的解析式为![]()
∴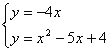
方程组无解,
∴D不在直线AC的左侧
当D在直线AC的右侧时,在x轴上取点M(2,0),则![]() ,
,
过点M作直线DM∥AC交抛物线于点D,则直线DM的解析式为![]() ,
,
∴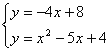
解得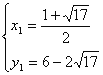 ,
,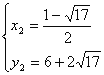
∴D(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
(3)解:设抛物线:![]() 的顶点为G,则点G(2.5,-2.25)关于x轴
的顶点为G,则点G(2.5,-2.25)关于x轴
对称点M的坐标为:M(2.5,2.25),
又∵N(0,1)解得直线MN:![]() ,
,
∵图象T顶点在直线MN上,
∴设图象T1顶点为
如图,由点A(1,0)与M(2.5,2.25)的坐标关系,得到点A的对应点![]() ,即
,即![]() 又BC:
又BC:![]()
当点K在BC上时,![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴点K在线段BC上,
设图象T1所在抛物线方程为:![]() ,点L为直线BC与抛物线的交点,则点L的坐标满足下列方程组:
,点L为直线BC与抛物线的交点,则点L的坐标满足下列方程组:
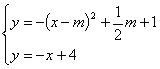
点L的横坐标是方程:![]() 的解
的解
当图象T1与直线BC相切时有:
![]() =0
=0
∴![]()
∴![]() ,
,
∵![]() ,
,
∴点L在图象T1上
∵![]() ,
,
∴点L在线段BC上
∴图象T1顶点横坐标的取值范围:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市建设地铁2号线,有一项工程原计划由甲工程队独立完成需要20天.在甲工程队施工4天后,为了加快工程进度,又调来乙工程队与甲工程队共同施工,结果比原计划提前10天完成任务.求:
⑴ 乙工程队独立完成这项工程需要的时间;
⑵ 甲、乙两工程队分别完成这项工程工作量的比.
-
科目: 来源: 题型:
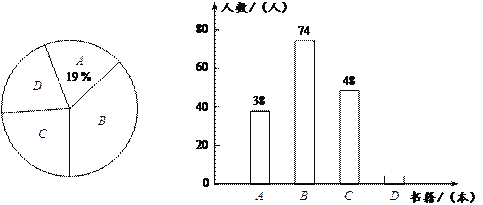
查看答案和解析>>【题目】某校对学生课外数阅读状况进行了一次问卷调查,并根据调查结果绘制了中学生每学期阅读课外书籍数量的统计图(不完整).设
 表示阅读书籍的数量(
表示阅读书籍的数量( 为正整数,单位:本),其中A:1≤
为正整数,单位:本),其中A:1≤ ≤2;B:3≤
≤2;B:3≤ ≤4;C:5≤
≤4;C:5≤ ≤6;D:
≤6;D: ≥7.请你根据两幅图提供的信息解答下列问题:
≥7.请你根据两幅图提供的信息解答下列问题:⑴ 本次共调查了多少名学生?
⑵ 补全条形统计图,并判断中位数在哪一组;
⑶ 计算扇形统计图中扇形D的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.0000210,结果是( )
A.2.10×10﹣4
B.2.10×10﹣5
C.2.1×10﹣4
D.2.1×10﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2xy2﹣3xy2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣3π,5
B.﹣3,6
C.﹣3π,7
D.﹣3π,6
相关试题

