【题目】“六一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
参考答案:
【答案】(1)设第一批玩具每套的进价是x元,
依据题意得![]() .
.
解得x=50.经检验,x=50是所列方程的解.
∴第一批玩具每套的进价是50元;
(2)设每套玩具的售价是a元,
依据题意得![]() .
.
解得x≥70.
∴总利润不低于25%,每套售价至少是70元.
【解析】试题分析:(1)、首先设每套的进价为x元,根据第一批和第二批的数量列出分式方程进行求解;(2)、首先求出第一批和第二批的数量,然后设出售价,根据利润率=(售价-进价)÷进价得出不等式,求出不等式的解.
试题解析:(1)、设第一批童装每套进价为x元,依题意得![]()
解得 x= 50,经检验,x=50是原方程的解。 ∴第一批童装每套进价为50元
(2)、设每套售价至少是y 元,依题意得第一批的数量为50件,第二批的数量为75件,
∴![]() 解得 y≥70
解得 y≥70
∴每套售价至少是70元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=10,点C,D在线段AB上,且AC=DB=2;点P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边三角形AEP和等边三角形PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,点G移动路径的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
(1)、求证:DE=BF;(2)、连接EF,写出图中所有的全等三角形.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线
 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在Rt△ABC中,AC=BC,∠C=90°,点D为AB边的中点,∠EDF=90°,△EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.当∠EDF绕点D旋转到DE⊥AC于点E时(如图①),易证S△DEF+S△CEF=
 S△ABC.
S△ABC.当∠EDF绕点D旋转到DE和AC不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的数量关系?请写出你的猜想,不需证明.

-
科目: 来源: 题型:
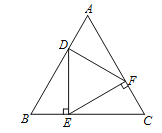
查看答案和解析>>【题目】如图,等边△ABC的边长为6,点D为AB上一点,DE⊥BC于点E,EF⊥AC于点F,连接DF.若△DEF也是等边三角形,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上海世博会会期为2010年5月1日至2010年10月31日。门票设个人票和团队票两大类。个人普通票160元/张,学生优惠票100元/张;成人团队票120元/张,学生团队票50元/张。
(1)如果2名老师、10名学生均购买个人票去参观世博会,请问一共要花多少元钱购买门票?
(2)用方程组解决下列问题:如果某校共30名师生去参观世博会,并得知他们都是以团队形式购买门票,累计花去2200元,请问该校本次分别有多少名老师、多少名学生参观世博会?
相关试题

