搜索
【题目】在学校组织的游艺晚会上，掷飞镖游戏规则如下：如图，掷到A区和B区的得分不同，A区为小圆内部分，B区为大圆内小圆外部分(掷中一次记一个点)．现统计小华、小明和小芳掷中与得分情况如图所示，依此方法计算小芳的得分为( )
A. 76分 B. 74分 C. 72分 D. 70分
参考答案：
【答案】B
【解析】
首先设掷到A区和B区的得分分别为x、y分，根据图示可得等量关系：①掷到A区5个的得分+掷到B区3个的得分=77分；②掷到A区3个的得分+掷到B区5个的得分=75分，根据等量关系列出方程组，解方程组即可得到掷中A区、B区一次各得多少分；由图示可得求的是掷到A区4个的得分+掷到B区4个的得分，根据解出的数代入计算即可．
设掷到A区和B区的得分分别为x、y分，依题意得：
,解得：
，
所以2x+6y=74，
答：依此方法计算小芳的得分为74．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（a，0）和B（0，b）满足
，分别过点A、B作x轴、y轴的垂线交于点C，如图，点P从原点出发，以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动．（1）写出A、B、C三点的坐标；
（2）当点P移动了6秒时，描出此时P点的位置，并写出点P的位置坐标；
（3）连结（2）中B、P两点，将线段BP向下平移h个单位（h＞0），得到B′P′，若B′P′将四边形OACB的周长分成相等的两部分，求h的值．
-
科目： 来源： 题型：
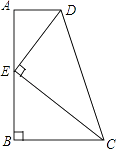
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=90°，E是AB上一点，且DE⊥CE．若AD=1，BC=2，CD=3，则CE与DE的数量关系正确的是（ ）
A.CE=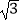
DE
B.CE=
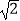DE
C.CE=3DE
D.CE=2DE -
科目： 来源： 题型：
查看答案和解析>>【题目】在等边△ABC中：
（1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；
（2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．
①依题意将图2补全；
②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证明PA=PM，只需证△APM是等边三角形；
想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．
-
科目： 来源： 题型：
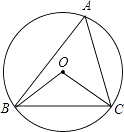
查看答案和解析>>【题目】如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC互补，则弦BC的长为（ ）
A.3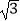
B.4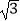
C.5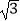
D.6 -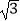
科目： 来源： 题型：
查看答案和解析>>【题目】用A、B两种机器人搬运大米，A型机器人比B型机器人每小时多搬运20袋大米，A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等．求A、B型机器人每小时分别搬运多少袋大米．
-
科目： 来源： 题型：
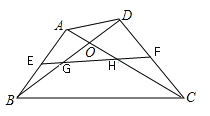
查看答案和解析>>【题目】如图，在四边形ABCD中，对角线AC、BD相交于点O，且AC=BD，E、F分别相交是AB、CD的中点，EF分别交BD、AC于点G、H。求证：OG=OH。
相关试题
