Question

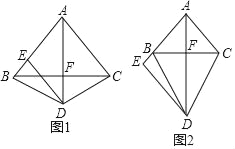
【题目】如图1，已知△ABC中，AB＝AC，点D是△ABC外一点（与点A分别在直线BC两侧），且DB＝DC，过点D作DE∥AC，交射线AB于E，连接AE交BC于F．

（1）求证：AD垂直BC；

（2）如图1，点E在线段AB上且不与B重合时，求证：DE＝AE；

（3）如图2，当点E在线段AB的延长线上时，写出线段DE，AC，BE的数量关系．

Answer 1

【答案】（1）见解析；（2）见解析；（3）DE＝AC+BE．

【解析】

（1）根据线段垂直平分线的判定定理得到直线AD是BC的垂直平分线，证明结论；

（2）证明△ABD≌△ACD，得到∠BAD＝∠CAD，根据平行线的性质得到∠BAD＝∠CAD，等量代换得到∠BAD＝∠EDA，根据等腰三角形的判定定理证明；

（3）仿照（2）的证明方法解答．

（1）∵AB＝AC，DB＝DC，

∴直线AD是BC的垂直平分线，

∴AD垂直BC；

（2）在△ABD和△ACD中，

，

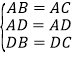∴△ABD≌△ACD，

∴∠BAD＝∠CAD，

∵DE∥AC，

∴∠EDA＝∠CAD，

∴∠BAD＝∠EDA，

∴DE＝AE；

（3）DE＝AC+BE．

由（2）得，∠BAD＝∠CAD，

∵DE∥AC，

∴∠EDA＝∠CAD，

∴∠BAD＝∠EDA，

∴DE＝AE，

∵AB＝AC，

∴DE＝AB+BE＝AC+BE．