搜索
【题目】计算：﹣22+ 
-2cos60°+ 
．
参考答案：
【答案】解：原式=﹣4+3﹣2× 
+3 =﹣4+3﹣1+3
=1．
【解析】分别根据有理数乘方的法则、数的开方法则、特殊角的三角函数值及负整数指数幂的运算法则计算出各数，再根据实数混合运算的法则进行计算即可．
【考点精析】本题主要考查了整数指数幂的运算性质和特殊角的三角函数值的相关知识点，需要掌握aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△B2D1C1的面积为S1 ， △B3D2C2的面积为S2 ， …，△Bn+1DnCn的面积为Sn ， 则Sn=（用含n的式子表示）．
-
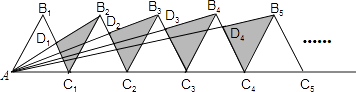
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，E、F分别是CD、AB延长线上的点，连结EF，分别交AD、BC于点G、H．若∠1=∠2，∠A=∠C，试说明AD//BC和AB//CD．请完成下面的推理过程，填写理由或数学式:
∵∠1=∠2，∠1=∠AGH（_________）
∴∠2=∠AGH（________）
∴AD//BC（________）
∴∠ADE=∠C（________）
∵∠A=∠C（已知）
∴∠ADE=_______（等量代换）
∴AB//CD（_______）
-
科目： 来源： 题型：
查看答案和解析>>【题目】为提倡全民健身活动， 某社区准备购买羽毛球和羽毛球拍供社区居民使用， 某体育用品商店羽毛球每盒 10 元， 羽毛球拍每副 40 元 ．该商店有两种优惠方案，方案一： 不购买会员卡时， 羽毛球享受 8.5 折优惠， 羽毛球拍购买 5 副（含5 副） 以上才能享受 8.5 折优惠， 5 副以下必须按定价购买；方案二： 每张会员卡 20 元， 办理会员卡时， 全部商品享受 8 折优惠 ． 设该社区准备购买羽毛球拍 6 副， 羽毛球
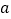盒， 请回答下列问题：（1）如果一位体育爱好者按方案一只购买了 4 副羽毛球拍，求他购买时所需要的费用；
（2）用含
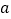的代数式分别表示该社区按方案一和方案二购买所需要的钱数；（3）①直接写出一个
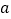的值， 使方案一比方案二优惠；②直接写出一个
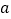的值， 使方案二比方案一优惠 ． -
科目： 来源： 题型：
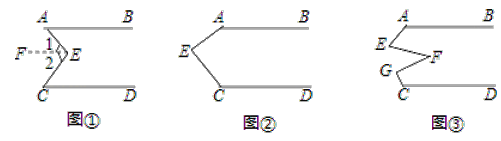
查看答案和解析>>【题目】（感知）如图①，AB∥CD，点E在直线AB与CD之间，连结AE、BE，试说明∠BEE+∠DCE＝∠AEC．下面给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式）：
解：如图①，过点E作EF∥AB
∴∠BAE＝∠1（ ）
∵AB∥CD（ ）
∴CD∥EF（ ）
∴∠2＝∠DCE
∴∠BAE+∠DCE＝∠1+∠2（ ）
∴∠BAE+∠DCE＝∠AEC
（探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠FGC+∠DCE＝360°；
（应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③．若∠EFG＝36°，则∠BAE+∠AEF+∠FGC+∠DCG＝ °．
-
科目： 来源： 题型：
查看答案和解析>>【题目】制了下列两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：
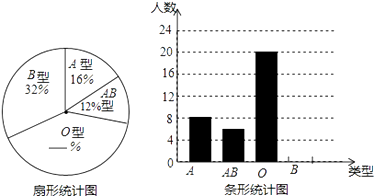
（1）该校七年级（1）班有多少名学生．
（2）求出扇形统计图中“O型”血所对扇形的圆心角的度数．
（3）将条形统计图中“B型”血部分的条形图补充完整． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．
（1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．
（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？
（3）如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本=进价×销售量）
相关试题
