Question

【题目】如图，正方形ABCD中，点E，F分别在AD，DC上，且△BEF为等边三角形，下列结论：

①DE=DF；②∠AEB=75°；③BE=DE；④AE+FC=EF．

其中正确的结论个数有（ ）

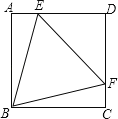
A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】根据三角形的全等的知识可以判断①的正误；根据角角之间的数量关系，以及三角形内角和为180°判断②的正误；根据等腰直角三角形的性质可判断③的正误；根据线段垂直平分线的知识可以判断④的正误.

解：∵四边形ABCD是正方形，∴AB=BC，∵△BEF是等边三角形，∴BBF，∵在Rt△ABE和Rt△BCF中，AB=BC，BE=BF，∴Rt△ABE≌△BCF（HL）∴AE=CF，AD=DC，AD-AE=CD-CF，

∴DE=DF，∴①正确；

∵DE=DF，∴△EDF是等腰直角三角形，∴∠DEF=45°，∵∠BEF=60°，∴∠AEB=75°，∴②正确；

∵BE=EF=DE，∴③正确；

如图，连接BD，交EF于G点，

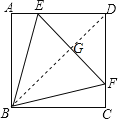
∴BD⊥EF，且BD平分EF，∵∠CBD≠∠DBF，∴CF≠FG，∴AE+FC≠EF，∴④错误；

故选C.

“点睛”本题考查了全等三角形的判定和性质，正方形的性质，等边三角形的性质，考本题中 求值△ABE≌△BCF是解题的关键.