【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于点N. 
(1)如图1,若CM∥BN交AD于点M.
①直接写出图1中所有与∠MCD相等的角:;(注:所找到的相等关系可以直接用于第②小题的证明过程
②过点C作CG⊥BN,交BN的延长线于点G,请先在图1中画出辅助线,再回答线段AM、CG、BN有怎样的数量关系,并给予证明 .
(2)如图2,若CM∥AB交BN的延长线于点M.请证明:∠MDN+2∠BDN=180°.
参考答案:
【答案】
(1)∠CAD,∠CBN;在图1中画出图形,如图所示, 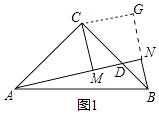
结论:AM=CG+BN,
证明:在△ACM和△BCG中,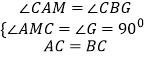 ,
,
∴△ACM≌△BCG,
∴CM=CG,AM=BG,
∵∠CMN=∠MNG=∠G=90°,
∴四边形MNGC是矩形,
∴CM=GN=CG,
∴AM=BG=BN+GN=BN+CG
(2)解:过点C作CE平分∠ACB,交AD于点E.

∵在△ACD和△BDN中,∠ACB=90°,AN⊥ND
∴∠4+∠ADC=90°=∠5+∠BDN
又∵∠ADC=∠BDN
∴∠4=∠5,
∵∠ACB=90°,AC=BC,CE平分∠ACB,
∴∠6=45°,∠2=∠3=45°
又∵CM∥AB,
∴∠1=∠6=45°=∠2=∠3,
在△ACE和△BCM中,
 ,
,
∴△ACE≌△BCM(ASA)
∴CE=CM
又∵∠1=∠2,CD=CD
∴∠CDE=∠CDM
又∵∠BDN=∠CDE,∠MDN+∠CDE+∠CDM=180°
∴∠MDN+2∠BDN=180°
【解析】解:(1)①∵CM∥BN,BN⊥AN,
∴∠CMD=∠N=90°,∠MCD=∠CBN,
∵∠ACB=90°,
∴∠ACM+∠CAD=90°,∠MCD+∠ACM=90°,
∴∠MCD=∠CAD,
所以答案是∠CAD、∠CBN.
②在图1中画出图形,如图所示,
结论:AM=CG+BN,
证明:在△ACM和△BCG中,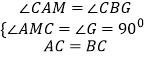 ,
,
∴△ACM≌△BCG,
∴CM=CG,AM=BG,
∵∠CMN=∠MNG=∠G=90°,
∴四边形MNGC是矩形,
∴CM=GN=CG,
∴AM=BG=BN+GN=BN+CG.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2.4,0,﹣2,2这四个数中,是负整数的是( )
A.﹣2.4B.﹣2C.0D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3s后,两点相距18个单位长度.已知点B的速度是点A的速度的5倍(速度单位:单位长度/s).
(1)求出点A、点B运动的速度,并在数轴上标出A,B两点从原点出发运动3s时的位置;
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)当A,B两点从(2)中的位置继续以原来的速度沿数轴向左运动的同时,另一点C从原点位置也向点A运动,当遇到点A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到点B追上点A时,点C立即停止运动.若点C一直以8个单位长度/s的速度匀速运动,则点C从开始运动到停止运动,行驶的路程是多少个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为( )

A.
B.
C.12
D.25 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)-82+72÷36 ;
(2)
 ;
;(3)
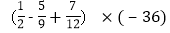 ;
;(4)
 ;
;(5)
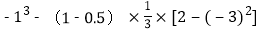 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,若∠BOD=28°
(1)求∠EOF的度数。 (2)求∠COF的度数。

相关试题

