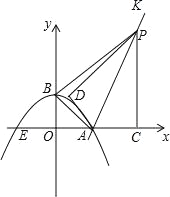
【题目】已知:如图,抛物线y=ax2+bx+2与x轴交于点A(4,0)、E(-2,0)两点,连结AB,过点A作直线AK⊥AB,动点P从A点出发以每秒![]() 个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
(1)求抛物线的解析式;
(2)当点D在△ABP的内部时,△ABP与△ADP不重叠部分的面积为S,求S与t之间的函数关系式,并直接写出t的取值范围;
(3)若线段AC的长是线段BP长的![]() ,请直接写出此时t的值;
,请直接写出此时t的值;
(4)是否存在这样的时刻,使动点D到点O的距离最小?若存在请直接写出这个最小距离;若不存在,说明理由.
参考答案:
【答案】(1)y=-![]() x2+
x2+![]() x+2,(2)S=-t2+5t(0<t<4)(3)t=
x+2,(2)S=-t2+5t(0<t<4)(3)t=![]() ;(4)
;(4)![]() .
.
【解析】
试题分析:(1)用待定系数法求出抛物线解析式;
(2)先根据点D在△APB内部,求出t的范围,然后用△APB减去△APC面积求出不重叠的部分面积;
(3)根据两点间的距离公式表示出BP,根据条件建立方程,求出时间;
(4)先判断出点D到点O的距离最小时的位置,然后用三角函数和勾股定理计算.
试题解析:(1)将A,B,E三点代入抛物线解析式中,得
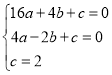 ,∴
,∴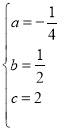
∴y=-![]() x2+
x2+![]() x+2,
x+2,
(2)∵A(4,0),B(0,2)
∴直线AB解析式为y=-![]() x+2,
x+2,
∵AB⊥AK,
∴直线AK解析式为y=2x+8,
∴tan∠PAC=![]() =2,
=2,
∵AP=![]() t,
t,
∴AC=t,PC=2t,
∵D在△ABP内部,
∴∠APB>∠APC,
∴tan∠APB>tan∠APC,
∴![]() ,
,
∴![]() ,
,
∴t<4,
∴0<t<4,
∴S=S△APB-S△APD
=S△APB-S△APC
=![]() ×AB×AP-
×AB×AP-![]() ×AC×PC
×AC×PC
=![]() ×2
×2![]() ×
×![]() t-
t-![]() ×t×2t
×t×2t
=-t2+5t(0<t<4)
(3)∵P(t+4,2t),
∴BP=![]() ,
,
∵线段AC的长是线段BP长的![]() ,
,
∴t=![]() ,
,
∴t=-![]() (舍)t=
(舍)t=![]()
(4)要使点D到O的距离最小,则有点D在OP上,此时记作D1
在Rt△OCP中,tan∠POC=![]() ,
,
在Rt△OCP中,tan∠AOC=![]() ,
,
∴![]() ,
,
∴OD1=![]() ,
,
根据勾股定理得,OD12+AD12=OA2,
∴(![]() )2+t2=16,
)2+t2=16,
∴t=-4(舍)t=![]() ,
,
∴AD1=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的课余生活,某中学在全校范围内随机抽取部分学生进行问卷调查,问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类.调查后将数据绘制成扇形统计图和条形统计图(如图所示).
(1)请根据所给的扇形图和条形图,直接填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在扇形统计图中,音乐类选项所在的扇形的圆心角的大小为 °;
(3)这所中学共有学生1200人,求喜欢音乐和美术类的课余生活共有多少人?
(4)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率.

-
科目: 来源: 题型:
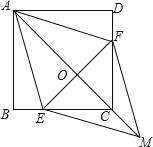
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣4b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2x+3)(2x-3)+(x-2)2-3x(x-1),其中x=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 169的平方根是13 B. 1.69的平方根是±1.3
C. (-13)的平方根是-13 D. -(-13)没有平方根
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A. 3,5,6B. 2,3,5C. 5,6,7D. 6,8,10
相关试题

