【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.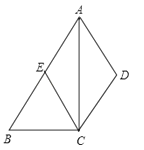
参考答案:
【答案】证明:(1)∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四边形AECD是平行四边形.
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四边形AECD是菱形;
(2)解:△ABC是直角三角形.
证法一:∵E是AB中点,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,
∴△ABC是直角三角形.
证法二:连DE,由四边形AECD是菱形,得到DE⊥AC,且平分AC,
设DE交AC于F,
∵E是AB的中点,且F为AC中点,
∴EF∥BC.∠AFE=90°,
∴∠ACB=∠AFE=90°,
∴BC⊥AC,
∴△ABC是直角三角形.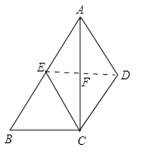
【解析】(1)根据两组对边分别平行证得四边形AECD是平行四边形,只需证明四边形AECD的两邻边相等即可.根据AC平分∠BAD,以及CE∥AD,易证得∠EAC=∠ECA,由此可知AE=CE,即四边形AECD是菱形;
(2)连DE,DE交AC于F,根据菱形的性质,对角线互相垂直且平分有:DE垂直平分AC,则EF是△ABC的中位线,有EF∥BC,则BC⊥AC,由此可证得△ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是一元二次方程x2﹣mx+2=0的一个解,则m的值是( )
A.﹣3
B.3
C.0
D.0或3 -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x.
(1)4x2=121;
(2)(x+2)3=125. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算,正确的是( )
A. ﹣
﹣  =
= 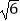
B.| ﹣2|=﹣
﹣2|=﹣ 
C. =2
=2 
D.( )﹣1=2
)﹣1=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.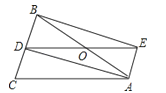
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.在一次抽奖活动中,“中奖概率是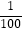 ”表示抽奖100次就一定会中奖
”表示抽奖100次就一定会中奖
B.随机抛一枚硬币,落地后正面一定朝上
C.同时掷两枚均匀的骰子,朝上一面的点数和为6
D.在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是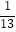
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元一次方程a(x﹣3)=2x﹣3a的解是x=3,则a= .
相关试题

