【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M.
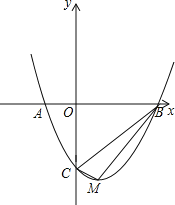
(1)求该抛物线的解析式及点M的坐标;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)△BCM为直角三角形;(3)符合条件的点有三个:O(0,0),P1(0,![]() ),P2(9,0).
),P2(9,0).
【解析】
试题分析:(1)已知抛物线图象上的三点坐标,可用待定系数法求出该抛物线的解析式;
(2)根据B、C、M的坐标,可求得△BCM三边的长,然后判断这三条边的长是否符合勾股定理即可;
(3)假设存在符合条件的P点;首先连接AC,根据A、C的坐标及(2)题所得△BDC三边的比例关系,即可判断出点O符合P点的要求,因此以P、A、C为顶点的三角形也必与△COA相似,那么分别过A、C作线段AC的垂线,这两条垂线与坐标轴的交点也符合点P点要求,可根据相似三角形的性质(或射影定理)求得OP的长,也就得到了点P的坐标.
解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=x2﹣2x﹣3;
(2)△BCM为直角三角形,理由为:
对于抛物线解析式y=x2﹣2x﹣3=(x﹣1)2﹣4,即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,即C(0,﹣3),
根据勾股定理得:BC=3![]() ,BM=2
,BM=2![]() ,CM=
,CM=![]() ,
,
∵BM2=BC2+CM2,
∴△BCM为直角三角形;
(3)若∠APC=90°,即P点和O点重合,如图1,
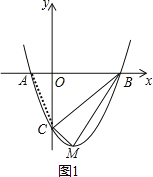
连接AC,
∵∠AOC=∠MCB=90°,且![]() =
=![]() ,
,
∴Rt△AOC∽Rt△MCB,
∴此时P点坐标为(0,0).
若P点在y轴上,则∠PAC=90°,如图2,过A作AP1⊥AC交y轴正半轴于P1,
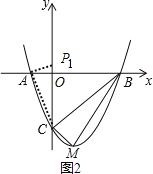
∵Rt△CAP1∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴点P1(0,![]() ).
).
若P点在x轴上,则∠PCA=90°,如图3,过C作CP2⊥AC交x轴正半轴于P2,
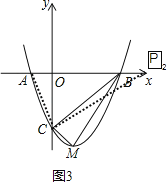
∵Rt△P2CA∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,AP2=10,
,AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,![]() ),P2(9,0).
),P2(9,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 面积相等的两个图形是全等图形 B. 形状相等的两个图形是全等图形
C. 周长相等的两个图形是全等图形 D. 全等图形的面积相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
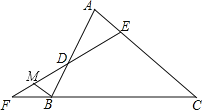
(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
则∠A=∠F,请说明理由.
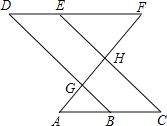
解:∵∠AGB=∠EHF
∠AGB= (对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC
∴∠ =∠DBA ( 两直线平行,同位角相等)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小兰在求一个多项式减去x2-3x+5时,误认为加上x2-3x+5,得到的答案是5x2-2x+4,则正确的答案是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数为勾股数的是( )
A. 6,12,13 B. 3,4,7 C. 8,15,16 D. 5,12,13
-
科目: 来源: 题型:
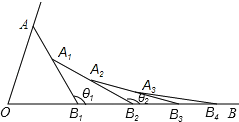
查看答案和解析>>【题目】如图所示,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律下去,记∠A2B1 B2=θ1,∠A3B2B3=θ2,…,∠An+1Bn Bn+1=θn,则θ2016﹣θ2015的值为( )
A.
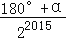 B.
B.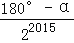 C.
C.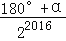 D.
D.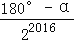
相关试题

