【题目】设二次函数![]() (
(![]() 为正常数)的图象与
为正常数)的图象与![]() 轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与![]() 轴交于C点.直线
轴交于C点.直线![]() 过M(0,m)(
过M(0,m)(![]() 且
且![]() )且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数
)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数![]() 的图象关于直线
的图象关于直线![]() 的对称图象与y轴交于点P.设直线PD与
的对称图象与y轴交于点P.设直线PD与![]() 轴交点为Q ,则:
轴交点为Q ,则:
⑴ 求A、C两点的坐标;
⑵ 求![]() 的值(用含m的代数式表示);
的值(用含m的代数式表示);
⑶ 是否存在实数m,使![]() ?若能,则求出相应的m的值;若不能,请说明理由.
?若能,则求出相应的m的值;若不能,请说明理由.
参考答案:
【答案】⑴ 点C的坐标为(0,2).点A坐标为(-1,0).
⑵ AD=![]() .
.
⑶当![]() >1时,才存在实数m使得
>1时,才存在实数m使得![]() ∽
∽![]() ,从而有
,从而有![]() ,此时
,此时![]() ;当0<
;当0<![]() 1时,不存在实数m使得
1时,不存在实数m使得![]() .
.
【解析】试题分析:(1)令y=0,可得A点的坐标,令x=0,可得C点的坐标;(2)根据A、C两个点的坐标求出直线AC的解析式,再求出点D的坐标,然后求出对应线段的长度,最后利用勾股定理即可求出AD;(3)要使CD·AQ=PQ·DE,因为∠PQA=∠PDE=∠CDE,所以只须△PQA∽△CDE,即须△PQA∽△PDE,分0 <m<1,1<m<2两个情况讨论求解即可.
试题解析:
⑴ 令y=0,可得:0=-![]() (x+1)(x-a),
(x+1)(x-a),
解得x1=-1,x2=a,
∵A在B的左侧,a>0,
∴A(-1,0),
令x=0,可得:y=-![]() ×(-a)=2,
×(-a)=2,
∴C(0,2).
故点C的坐标为(0,2),点A坐标为(-1,0).
(2)
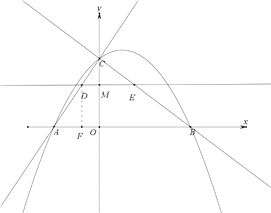
作DF⊥AB于点F,
∵A(-1,0),C(0,2),
∴直线AC解析式为:y=2x+2,
令y=m,m=2x+2,x=![]() -1,
-1,
∴D(![]() -1,m),
-1,m),
∴FO=1-![]() ,
,
∴AF=![]() ,
,
∵DF=m,
∴AD=![]() m.
m.
⑶连接AP、PE,
要使CD·AQ=PQ·DE,∵∠PQA=∠PDE=∠CDE,
∴只须△PQA∽△CDE,即须△PQA∽△PDE.

当0 <m<1时,点P在x轴下方,此时∠PQA显然为钝角,
而∠PDE显然为锐角,故此时不能有△PQA∽△CDE.
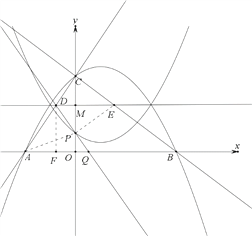
当1<m<2时,△PQA∽△PDE时,A、P、E三点共线,
∴△APO∽△EPM,
∴![]() =
=![]() ,
,
∵B(a,0),C(0,2),
∴直线BC解析式为:y=-![]() x+2,
x+2,
令![]() =
=![]() ,
,![]() =-
=-![]() +2,
+2,![]() =a-
=a-![]() ,
,
∴E(a-![]() ,m),
,m),
∴ME= a-![]() ,
,
∵CO=2,MO=m,
∴PM=CM=2-m,
∴PO=2m-2,
∴![]() =
=![]() ,
,
∴ ![]() ,而此时1<m<2,
,而此时1<m<2,
∴![]() ,
,
∴a>1.
综上所述,当a>1时,才存在实数m使得△PQA∽△CDE,从而有CD·AQ=PQ·DE,此时![]() ;当0<a≤1时,不存在实数
;当0<a≤1时,不存在实数![]() 使得CD·AQ=PQ·DE.
使得CD·AQ=PQ·DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果节约10吨水记作+10吨,那么浪费5吨水记作吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2﹣2a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kxy+64y2是一个完全平方式,则k=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市建设地铁2号线,有一项工程原计划由甲工程队独立完成需要20天.在甲工程队施工4天后,为了加快工程进度,又调来乙工程队与甲工程队共同施工,结果比原计划提前10天完成任务.求:
⑴ 乙工程队独立完成这项工程需要的时间;
⑵ 甲、乙两工程队分别完成这项工程工作量的比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对学生课外数阅读状况进行了一次问卷调查,并根据调查结果绘制了中学生每学期阅读课外书籍数量的统计图(不完整).设
 表示阅读书籍的数量(
表示阅读书籍的数量( 为正整数,单位:本),其中A:1≤
为正整数,单位:本),其中A:1≤ ≤2;B:3≤
≤2;B:3≤ ≤4;C:5≤
≤4;C:5≤ ≤6;D:
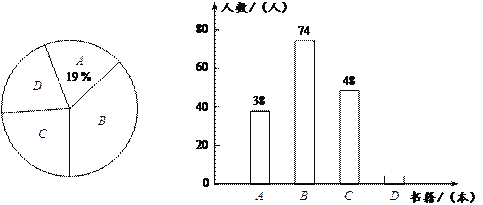
≤6;D: ≥7.请你根据两幅图提供的信息解答下列问题:
≥7.请你根据两幅图提供的信息解答下列问题:⑴ 本次共调查了多少名学生?
⑵ 补全条形统计图,并判断中位数在哪一组;
⑶ 计算扇形统计图中扇形D的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要元.
相关试题

