Question

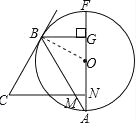
【题目】如图，CB是⊙O的切线，AF是⊙O的直径，CN⊥AF于点N，BG⊥AF于点G，连接AB交CN于点M．

（1）写出与点B有关的三条不同类型的结论．(2)、若AG=3FG，求tanA的值．

Answer 1

【答案】(1)、OB⊥BC，AB⊥BF，OA=OB，BC=CM；(2)、.

【解析】

试题分析：(1)、由切线的性质和圆的性质即可得出结论；(2)、连接OB，由AG=3FG，推出FG=OG=OF，得到OG=OB，根据直角三角形的性质得到∠GBO=30°，即可求得∠A==30°，于是得到结果．

试题解析：(1)、与点B有关的结论：OB⊥BC，AB⊥BF，OA=OB，BC=CM；

(2)、如图，连接OB，∵AG=3FG，∴FG=OG=OF，∴OG=OB，∵BG⊥AF，∴∠GBO=30°，

∴∠BOG=60°，∵OB=OA，∴∠A==30°，∴tan∠A=．