搜索
【题目】如图，AB与CD交于点O，OE平分∠AOC，点F为AB上一点(不与点A及O重合)，过点F作FG∥OE，交CD于点G，若∠AOD＝110°，则∠AFG度数为_____．
参考答案：
【答案】35°或145
【解析】
分两种情况，如图（1）点F在OB上，图（2）点F在OA上，再据角平分线的性质以及平行线性质解题.
如图（1）点F在OB上：图（1）
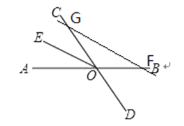
∵∠AOD＝110°，OE平分∠AOC，
∴∠AOE＝
=
（180°-110°）=35°，
∵FG∥OE，
∴∠AFG=∠AOE=35°；
如图（2）点F在OA上：图（2）
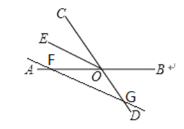
∵∠AOD＝110°，OE平分∠AOC，
∴∠AOE＝=（180°-110°）=35°，
∵FG∥OE，
∴∠AFG=∠EOG=∠AOD+∠AOE=110°+35°=145°.
故答案为：35°或145°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知□ABCD，AB//x轴，AB=6，点A的坐标为（1，-4），点D的坐标为（-3,4），点B在第四象限，点P是□ABCD边上的一个动点.
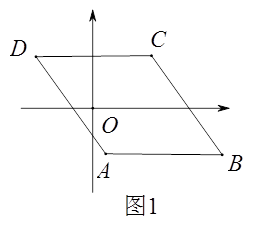
（1）若点P在边BC上，PD=CD，求点P的坐标.
（2）若点P在边AB，AD上，点P关于坐标轴对称的点Q落在直线y=x-1上，求点P的坐标.
（3）若点P在边AB，AD，CD上，点G是AD与y轴的交点，如图2，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，求点P的坐标（直接写出答案）. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在下列条件中，不能作为判断△ABD≌△BAC的条件是（ )
A. ∠D＝∠C，∠BAD＝∠ABC B. ∠BAD＝∠ABC，∠ABD＝∠BAC
C. BD＝AC，∠BAD＝∠ABC D. AD＝BC，BD＝AC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB∥CD，则∠A、∠C、∠E、∠F满足的数量关系是( )
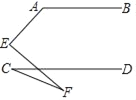
A. ∠A＝∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F＝180°
C. ∠A﹣∠E+∠C+∠F＝90° D. ∠A+∠E+∠C+∠F＝360°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，按以下步骤作图：①分别以A、B为圆心，大于
AB的长为半径画弧，两弧相交于点M、N；②作直线MN交AC于点D，连接BD．若CD=CB，∠A=35°，则∠C等于（ ）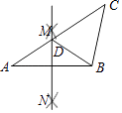 
A.40°
B.50°
C.60°
D.70° -
科目： 来源： 题型：
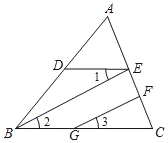
查看答案和解析>>【题目】已知：如图，BE∥GF，∠1＝∠3，∠DBC＝70°，求∠EDB的大小．
阅读下面的解答过程，并填空(理由或数学式)
解：∵BE∥GF(已知)
∴∠2＝∠3( )
∵∠1＝∠3( )
∴∠1＝( )( )
∴DE∥( )( )
∴∠EDB+∠DBC＝180°( )
∴∠EDB＝180°﹣∠DBC(等式性质)
∵∠DBC＝( )(已知)
∴∠EDB＝180°﹣70°＝110°
-
科目： 来源： 题型：
查看答案和解析>>【题目】某小组在“用频率估计概率”的实验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的实验最有可能的是（ ）
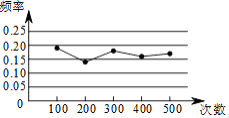
A.袋子中有1个红球和2个黄球，它们只有颜色上的区别，从中随机地取出一个球是黄球
B.掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6
C.在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
D.掷一枚质地均匀的硬币，落地时结果是“正面向上”
相关试题
