【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE∠B.

(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并证明你的猜想.
参考答案:
【答案】(1)∠B=30°;(2)6cm;(3)ED⊥AB.
【解析】
试题分析:(1)先由角平分线的定义及已知条件得出∠CAE=∠EAB=∠B,再根据直角三角形两锐角互余得出∠CAE+∠EAB+∠B=3∠B=90°,那么∠B=30°;
(2)根据30°角所对的直角边等于斜边的一半得出AB=2AC=6cm;
(3)先由∠EAB=∠B,根据等角对等边得出EB=EA,又ED平分∠AEB,根据等腰三角形三线合一的性质得到ED⊥AB.
解:(1)∵AE是△ABC的角平分线,
∴∠CAE=∠EAB,
∵∠CAE=∠B,
∴∠CAE=∠EAB=∠B.
∵在△ABC中,∠C=90°,
∴∠CAE+∠EAB+∠B=3∠B=90°,
∴∠B=30°;
(2)∵在△ABC中,∠C=90°,∠B=30°,AC=3cm,
∴AB=2AC=6cm;
(3)猜想:ED⊥AB.理由如下:
∵∠EAB=∠B,
∴EB=EA,
∵ED平分∠AEB,
∴ED⊥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是_________________________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论,①abc<0; ②2a+b=0;③b2﹣4ac<0;④a+b+c>0;⑤a﹣b+c<0.其中正确的结论有(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间2015年7月31日,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会举办权.北京也创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市,张家口也成为本届冬奥会的协办城市.近期,新建北京至张家口铁路可行性研究报告已经获得国家发改委批复,同意新建北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )

A. 95° B. 65°
C. 50° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB和CD相交于O点,OE⊥AB,∠1=55°,则∠BOD= 度;若OF平分∠DOB,则∠EOF的度数是 度.
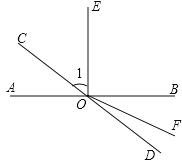
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形,寻找对顶角(不含平角).
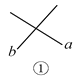
(1)如图①,图中共有____对对顶角;
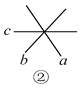
(2)如图②,图中共有____对对顶角;
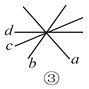
(3)如图③,图中共有____对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角对数的关系,猜想:若有n条直线相交于一点,则共可形成__________对对顶角;
(5)若有180条直线相交于一点,则可形成________对对顶角.
相关试题

