【题目】如图，直线y=kx+b过x轴上的点A（2，0），且与抛物线交于B，C两点，点B坐标为（1，1）.

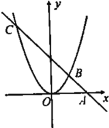
（1）求直线与抛物线对应的函数表达式；

（2）当时，请根据图象写出自变量x的取值范围；

（3）抛物线上是否存在一点D，使？若存在，求出D点坐标；若不存在，请说明理由

【答案】（1）y＝x＋2，y＝x2（2）-2＜x＜1（3） (，3)或(，3)

【解析】

（1）已知直线AB经过A（2，0），B（1，1），设直线表达式为y＝ax＋b，可求直线解析式；将B（1，1）代入抛物线y＝ax2可求抛物线解析式；

（2）求出B,C的坐标，根据图像即可求解；

（3）已知A，B，C三点坐标，根据作差法可求△OBC的面积，在△DOA中，已知面积和底OA，可求OA上的高，即D点纵坐标，代入抛物线解析式求横坐标，得出D点坐标．

（1）设直线AB关系式为y＝kx＋b

∵A（2，0），B（1，1）都在直线y＝kx＋b的图象上，

∴解得，

∴直线AB关系式为y＝x＋2，

∵点B（1，1）在y＝ax2的图象上，

∴a＝1，其关系式为y＝x2；

（2）由题意得，

解得或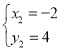

∴C（-2，4）

由图像可知表示一次函数在二次函数上方，

故x的取值为-2＜x＜1；

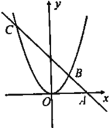
（3）如图，存在点D，设D（x，x2），

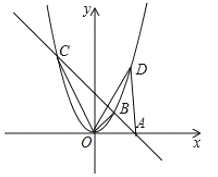
∴S△OAD＝|OA||yD|＝×2×x2＝x2

∵C（2，4），

∴S△BOC＝S△AOCS△OAB＝×2×4×2×1＝3，

∵S△BOC＝S△OAD，

∴x2＝3，

解得x＝±，

∴点D坐标为(，3)或(，3)．

关闭