搜索
【题目】已知x3m＝2，y2m＝3，求(x2m)3＋(ym)6－(x2y)3m·ym的值．
参考答案：
【答案】－5.
【解析】根据幂的乘方的性质将式子进行变形，然后代入求解即可．
试题分析：
因为x3n=2，y2n=3，
所以(x2n)3+(yn)6(x2y)3nyn
=x6n+y6nx6ny3nyn
=(x3n)2+(y2n)3(x3n)2(y2n)2
=22+3322×32
=4+274×9
=5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式由左边到右边的变形中，是分解因式的为（ ）
A. a（x+y）=ax+ay B. x2-4x+4=x（x-4）+4
C. 10x2-5x=5x（2x-1） D. x2-16+3x=（x-4）(x+4)+3x
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，点E、F分别在AB、BC上，△DEF为等腰直角三角形，∠DEF=90°，AD+CD=10，AE=2，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD中，∠B＝30°，AB ≠ BC ，将△ABC沿AC翻折至△AB′C ，连结B ′D. 若
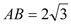，∠AB ′D＝75°，则BC =_____________．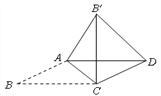
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：3x2﹣27= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某个数的平方根分别是a＋3和2a＋15，则这个数为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明是个爱动脑筋的学生，在学习了解直角三角形以后，一天他去测量学校的旗杆DF的高度，此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米．
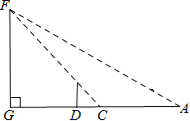
（1）若旗杆的高度FG是a米，用含a的代数式表示DG．
（2）小明从点C后退6米在A的测得旗杆顶点F的仰角为30°，求旗杆FG的高度．（点A、C、D、G在一条直线上，
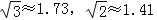，结果精确到0.1）
相关试题
