【题目】已知关于x的一元二次方程x2+(2m+3)x+m2=0有两个不相等的实数根,
(1)求m的取值范围
(2)若α,β是方程的两个实数根,且满足![]() =﹣1,求m的值.
=﹣1,求m的值.
参考答案:
【答案】(1)m>﹣![]() ;(2)m=3.
;(2)m=3.
【解析】
(1)根据方程有两个相等的实数根可知△>0,求出m的取值范围即可;
(2)根据根与系数的关系得出α+β与αβ的值,代入代数式进行计算即可.
(1)∵关于x的一元二次方程x2+(2m+3)x+m2=0有两个不相等的实数根,
∴△>0,即△=(2m+3)2﹣4m2>0,解得m>﹣![]() ;
;
(2)∵α,β是方程的两个实数根,
∴α+β=﹣(2m+3),αβ=m2.
∵![]() ,
,
∴﹣(2m+3)=﹣m2,解得m1=3,m2=﹣1(舍弃).
∴m=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P是以C(﹣
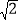 ,
,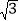 )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.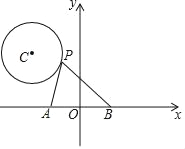
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AM为⊙O的切线,A为切点,过⊙O上一点B作BD⊥AM于点D,BD交⊙O于C,OC平分∠AOB.
(1)求∠AOB的度数;
(2)若线段CD的长为2cm,求
 的长度.
的长度.
-
科目: 来源: 题型:
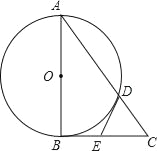
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)求证:4DE2=CDAC.
-
科目: 来源: 题型:
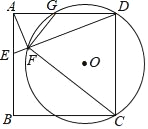
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
-
科目: 来源: 题型:
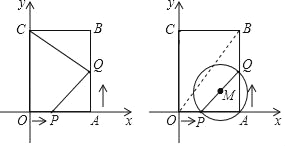
查看答案和解析>>【题目】如图,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿OA以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当t=2时,线段PQ的中点坐标为 .
(2)当△CBQ与△PAQ相似时,求t的值;
(3)连接OB,若以PQ为直径作⊙M,则在运动过程中,是否存在某一时刻t,使得⊙M与OB相切,若存在,求出时间t;若不存在,请说明理由.
相关试题

