【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位向终点
个单位向终点![]() 匀速运动(点
匀速运动(点![]() 不与
不与![]() 、
、![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() .以
.以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)直接写出![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形不是矩形时,求
重叠部分图形不是矩形时,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)沿直线![]() 将矩形
将矩形![]() 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的![]() 的值.
的值.
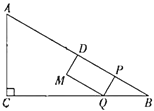
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3) ;(4)
;(4)![]() 或
或![]()
![]() .
.
【解析】
(1)根据P点的运动速度和BD的长度即可出结果;
(2)画出图象,根据三角形的相似求出各个线段长,即可解决;
(3)分情况讨论,矩形![]() 与
与![]() 重叠部分面积即为矩形面积减去△ABC外部的小三角形面积,通过三角函数计算出各边长求面积即可;
重叠部分面积即为矩形面积减去△ABC外部的小三角形面积,通过三角函数计算出各边长求面积即可;
(4)要想使被直线分割成的两部分能拼成不重叠且无缝隙的图形恰好是三角形,则需要被分割的是两个至少有一条相等边长的直角三角形,或者直线正好过正方形一条边的中点,分情况画图求解即可.
解:(1)∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
P从B运动到点D所需时间为1s,
由题意可知![]() ,
,
![]() ;
;
(2)如图所示,
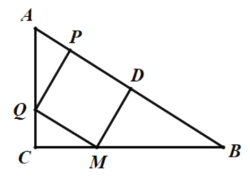
由题意得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由四边形![]() 是矩形可知,∠QPD=∠MDP=90°,PQ=DM,即∠APQ=∠BDM=90°,
是矩形可知,∠QPD=∠MDP=90°,PQ=DM,即∠APQ=∠BDM=90°,
∵∠B=∠B,∠BDM=∠ACB=90°,
∴△MDB∽△ACB,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]()
∵∠A=∠A,∠APQ=∠ACB=90°,
∴△APQ∽△ACB,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
(3)当![]() 时,如图,DM交BC于点F,
时,如图,DM交BC于点F,

由矩形可知PD∥QM,∴∠FQM=∠B=30°,
此时![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
![]() ,
,
同理![]() ,
,![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,如图,DM交BC于点F,QM交BC于E,
时,如图,DM交BC于点F,QM交BC于E,
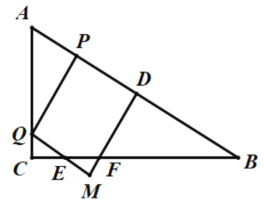
![]() ,由题意可知∠A=60°,
,由题意可知∠A=60°,
![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
综上所述: ;
;
(4)如图所示,当Q与C重合时,满足条件,

由前面解题过程可知此时![]() ,
,
当PQ=DM时,此时直线CD正好过QM的中点,满足条件,

此时![]() ,
,
当直线CD正好过PQ的中点G时,满足条件,如图,

由前面计算可知![]() ,则
,则![]() ,
,
![]() ,
,
解得![]() ,
,
综上所述,![]() 或
或![]()
![]() .
.

