Question

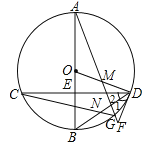
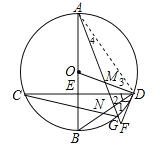
【题目】如图，在⊙O中，直径AB经过弦CD的中点E，点M在OD上，AM的延长线交⊙O于点G，交过D的直线于F，∠1=∠2，连结BD与CG交于点N．

（1）求证：DF是⊙O的切线；

（2）若点M是OD的中点，⊙O的半径为3，tan∠BOD=，求BN的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】试题分析：（1）根据切线的判定定理得出∠1+∠BDO=90°，即可得出答案；

（2）利用已知得出∠3=∠2，∠4=∠C，再利用相似三角形的判定方法得出即可；根据已知得出OE的长，进而利用勾股定理得出ED，AD，BD的长，即可得出CD，利用相似三角形的性质得出NB的长即可．

试题解析：解：（1）证明：∵直径AB经过弦CD的中点E，∴AB⊥CD， ，∴∠BOD=2∠2．

∵∠1=∠2，∠BOD+∠ODE=90°，∴∠ODE+∠1+∠2=90°，∴∠ODF=90°，∴DF是⊙O的切线；

（2）解：∵AB是⊙O直径，∴∠ADB=∠FDO=90°，∴∠ADB﹣∠BDO=∠FDO﹣∠BDO，即∠3=∠1，∴∠3=∠2，∵∠4=∠C，∴△ADM∽△CDN；

∵⊙O的半径为3，即AO=DO=BO=3，在Rt△DOE中，tan∠BOD=，cos∠BOD=，∴OE=DOcos∠BOD=3×=1，由此可得：BE=2，AE=4，由勾股定理可得：DE==，AD==，BD==，∵AB是⊙O直径，AB⊥CD，∴由垂径定理得：CD=2DE=，∵△ACM∽△DCN，∴，∵点M是DO的中点，DM=AO=×3=，∴DN===，∴BN=BD﹣DN==．