搜索
【题目】已知：在平面直角坐标系中，抛物线 y=ax2 -2ax+4(a<0) 交 x 轴于点 A、B，与 y 轴交于点 C，AB=6．
（1）如图 1，求抛物线的解析式；
（2） 如图 2，点 R 为第一象限的抛物线上一点，分别连接 RB、RC，设△RBC 的面积为 s，点 R 的横坐标为 t，求 s 与 t 的函数关系式；
（3）在（2）的条件下，如图 3，点 D 在 x 轴的负半轴上，点 F 在 y 轴的正半轴上，点 E 为 OB 上一点，点 P 为第一象限内一点，连接 PD、EF，PD 交 OC 于点 G，DG=EF，PD⊥EF，连接 PE，∠PEF=2∠PDE，连接 PB、PC，过点R 作 RT⊥OB 于点 T，交 PC 于点 S，若点 P 在 BT 的垂直平分线上，OB-TS=
，求点 R 的坐标．
【答案】（1）
；（2）
；（3）R（2，4）或R（
，
）
【解析】
（1）先求出抛物线的对称轴，再根据A、B关于抛物线对称轴对称和AB的长即可求出A、B的坐标，然后代入解析式即可；
（2）过点R作x轴的垂线，交BC于点M，根据题意可得点R的坐标为
，点M的横坐标为t,然后求出点C的坐标，利用待定系数法求出直线BC的解析式，即可求出点M的坐标，最后利用“铅垂高，水平宽”即可求出结论；
（3）设PG与EF交于点H，连接EG，设R点的坐标为，则OT=t，根据题意求出点S的坐标，即可求出直线SC的解析式，然后根据全等三角形的判定及性质、垂直平分线的判定、三线合一证出OP平分∠EOG，可得点P的横纵坐标相等，再结合已知条件即可求出点P的坐标，代入直线SC的解析式即可求出t，从而求出点R的坐标．
解：（1）抛物线 y=ax2 -2ax+4(a<0)的对称轴为x=
∵AB=6，A、B关于x=1对称
∴点A的横坐标为1－
=-2，点B的横坐标为1＋=4
∴点A的坐标为（-2,0），点B的坐标为（4,0）
将点A的坐标代入y=ax2 -2ax+4中，得
0=4a＋4a＋4
解得：a=
∴抛物线的解析式为；
（2）过点R作x轴的垂线，交BC于点M
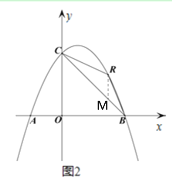
∵点 R 的横坐标为 t
∴点R的坐标为，点M的横坐标为t
将x=0代入中，解得y=4
∴点C的坐标为（0,4）
设直线BC的解析式为y=kx＋b
将点B、C的坐标代入，得
解得：
∴直线BC的解析式为y=-x＋4
∴点M的坐标为（t，-t＋4）
∴RM=
∴s=
RM·（xB－xC）=
·（4－0）=
（3）设PG与EF交于点H，连接EG
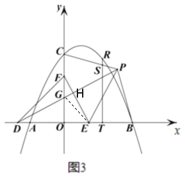
设R点的坐标为，则OT=t
∵OB-TS=
，OB=4
∴TS=
∴点S的坐标为（t，）
设直线SC的解析式为：y=mx＋n
将S、C的坐标代入，得
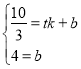
解得：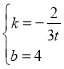 
∴直线SC的解析式为
∵∠DOG=∠FOE=∠DHE=90°
∴∠ODG＋∠HEO=90°，∠OFE＋∠HEO=90°
∴∠ODG=∠OFE
∵DG=FE
∴△ODG≌△OFE
∴OG=OE，
∴点O在GE的中垂线上，△OGE为等腰直角三角形
∴∠GEO=∠OGE=45°
∴∠PGE=∠GEO＋∠PDE=45°＋∠PDE，∠FEG=∠OGE－∠OFE=45°－∠PDE
∵∠PEF=2∠PDE
∴∠PEG=∠PEF＋∠FEG=2∠PDE＋45°－∠PDE=45°＋∠PDE
∴∠PGE=∠PEG
∴PG=PE
∴点P在EG的中垂线上
∴OP垂直平分EG
∴OP平分∠EOG
∴点P的横、纵坐标相等
∵点 P 在 BT 的垂直平分线上
∴点P的坐标为（
）
将点P的坐标代入直线SC的解析式中，得
解得：
经检验：均为原方程的解
当t=2时，点R的坐标为（2,4）；
当t=时，点R的坐标为（，）
综上所述：R（2，4）或R（，）
