【题目】已知关于x的一元二次方程x2+2(k+1)x+k2+2=0有两个实根x1,x2.
(1)求实数k的取值范围;
(2)若实数k能使x1﹣x2=2![]() ,求出k的值.
,求出k的值.
参考答案:
【答案】(1)k≥![]() (2)3
(2)3
【解析】试题分析:(1)根据方程的系数结合根的判别式△≥0,即可得出关于k的一元一次不等式,解之即可得出实数k的取值范围;
(2)根据根与系数的关系可得出x1+x2=﹣2(k+1)、x1x2=k2+2,结合(x1﹣x2)2=(x1+x2)2﹣4x1x2=(2![]() )2,即可得出关于k的一元一次方程,解之即可得出结论.
)2,即可得出关于k的一元一次方程,解之即可得出结论.
试题解析:解:(1)∵原方程有两个实数根,∴△=[2(k+1)]2﹣4(k2+2)>0,解得:k≥![]() .
.
(2)∵x1、x2是方程x2+2(k+1)x+k2+2=0有两个实根,∴x1+x2=﹣2(k+1),x1x2=k2+2,∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(2![]() )2,∴[﹣2(k+1)]2﹣4(k2+2)=20,即8k﹣24=0,解得:k=3.
)2,∴[﹣2(k+1)]2﹣4(k2+2)=20,即8k﹣24=0,解得:k=3.
∵k>![]() ,∴k的值为3.
,∴k的值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市高中招生体育考试前教育部门为了解全市九年级男生考试项目的选择情况(每人限选一项),对全市部分九年级男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)将上面的条形统计图补充完整;
(2)假定全市九年级毕业学生中有5500名男生,试估计全市九年级男生中选“50米跑”的人数有多少人?
(3)甲、乙两名九年级男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球和立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
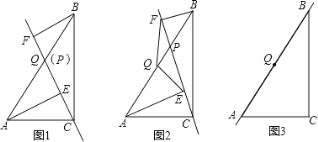
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
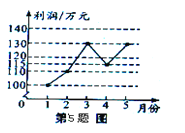
A. 1~2月份利润的增长快于2~3月份分利润的增长
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~5月份利润的的众数是130万元
D. 1~5月份利润的中位数为120万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在反比例函数
 (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.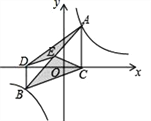
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
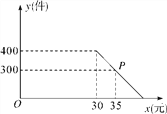
查看答案和解析>>【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
相关试题

