【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
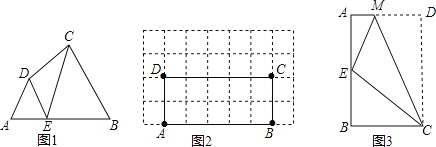
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
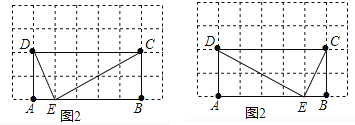
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
参考答案:
【答案】(1)点E是四边形ABCD的边AB上的相似点.理由见解析;
(2)见解析;
(3)![]() .
.
【解析】
试题分析:(1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
(2)根据两个直角三角形相似得到强相似点的两种情况即可.
(3)因为点E是梯形ABCD的AB边上的一个强相似点,所以就有相似三角形出现,根据相似三角形的对应线段成比例,可以判断出AE和BE的数量关系,从而可求出解.
解:(1)点E是四边形ABCD的边AB上的相似点.
理由:∵∠A=55°,
∴∠ADE+∠DEA=125°.
∵∠DEC=55°,
∴∠BEC+∠DEA=125°.
∴∠ADE=∠BEC.(2分)
∵∠A=∠B,
∴△ADE∽△BEC.
∴点E是四边形ABCD的AB边上的相似点.
(2)作图如下:
(3)∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=![]() ∠BCD=30°,
∠BCD=30°,
∴BE=![]() CE=
CE=![]() AB.
AB.
在Rt△BCE中,tan∠BCE=![]() =tan30°,
=tan30°,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个
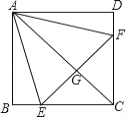
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
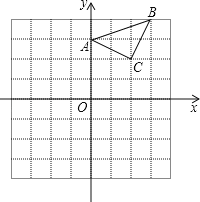
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
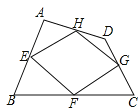
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形.
(3)你学过的哪种特殊四边形的中点四边形是菱形? .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校羽毛球队需要购买6支羽毛球拍和x盒(x>6)羽毛球,羽毛球拍市场价为200元/支,羽毛球为30元/盒。甲商场优惠方案为:所有商品9折。乙商场优惠方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售。
(1)分别用x的代数式表示在甲商场和乙商场购买所有物品的费用。
(2)当x=20时,分别计算在甲商场和乙商场购买所需费用。
-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地一天早晨气温为-1℃,中午上升了8℃,夜间又下降了10℃,那么该地这天夜间的气温是_____.
相关试题

